Gestión de Carteras y MPT: Creando la Frontera Eficiente con Análisis Cuantitativo en la Era Cripto

Por el Equipo de Análisis cripTor

Introducción: Por qué la Optimización del Portafolio es Clave en 2025

En el entorno de alta volatilidad y rendimientos inciertos de 2025, especialmente en los mercados de criptoactivos y acciones tecnológicas, la intuición no es suficiente. El inversor moderno requiere herramientas matemáticas sólidas para balancear el riesgo y el rendimiento.

Desde su publicación en 1952 por el economista Harry Markowitz, la Teoría Moderna del Portafolio (MPT) ha sido el pilar fundamental de la gestión de activos. La MPT transformó la inversión de una selección de acciones individuales a la gestión de la diversificación del riesgo de una cartera completa.

Es difícil exagerar la revolución que supuso el trabajo de Markowitz. Antes de él, la gente simplemente buscaba el activo con el mayor rendimiento. Él nos obligó a pensar en el riesgo no solo como un peligro, sino como una variable que podemos y debemos optimizar.

En este análisis detallado, el Equipo de Análisis cripTor revisa los pilares de la MPT, explica cómo construir la crucial Frontera Eficiente y, más importante aún, ofrece una perspectiva crítica sobre sus limitaciones en los mercados de alta frecuencia actuales, especialmente cómo podemos integrarla con las herramientas de la Inteligencia Artificial y la tecnología blockchain para una gestión más robusta.

1. Los Pilares Fundamentales de la Teoría Moderna del Portafolio (MPT)

La MPT establece que un inversor racional siempre buscará maximizar el rendimiento esperado para un nivel de riesgo dado, o minimizar el riesgo para un rendimiento esperado dado. Esto se logra mediante la diversificación. Markowitz nos dio una hoja de ruta matemática para evitar poner todos los huevos en la misma canasta.

1.1. Los Conceptos Centrales y la Importancia de la Covarianza

La fortaleza de la MPT radica en la relación estadística entre los activos:

Rendimiento Esperado ($E(R_p)$): El rendimiento que un inversor espera de la cartera, calculado como la media ponderada de los rendimientos de cada activo.
Riesgo (Varianza o Desviación Estándar $\sigma_p$): La medida de la volatilidad del portafolio.
Covarianza ($\rho_{ij}$): Es el factor más crítico. Mide cómo se mueven dos activos entre sí. Si Bitcoin y Ethereum tienen una correlación cercana a +1, no están diversificando. Si el Oro y el Dólar tienen una correlación negativa, están diversificando. Añadir un activo que se mueve en dirección opuesta al resto de la cartera reduce drásticamente el riesgo general.

1.2. De la Diversificación Simple a la Optimización Estratégica

Según la MPT, el riesgo total de una cartera se divide en dos, lo que nos da nuestra primera estrategia de gestión de riesgo:

Riesgo No Sistemático (Diversificable): Específico de un activo o empresa. Es el riesgo de que la gerencia de una sola empresa falle. Este riesgo se puede eliminar por completo a través de la diversificación adecuada.
Riesgo Sistemático (No Diversificable): Es el riesgo inherente al mercado completo (por ejemplo, una crisis global o un cambio en la política de tasas de interés). Es medido por el coeficiente Beta y no puede ser eliminado.

La MPT nos enseña que el riesgo que realmente importa para la inversión a largo plazo es el sistemático. Nuestro trabajo como gestores de cartera es eliminar primero todo el riesgo no sistemático, y luego optimizar la exposición al riesgo sistemático según el perfil del cliente.

2. Modelización: El Santo Grial de la Inversión (La Frontera Eficiente)

La meta de la MPT es identificar la Frontera Eficiente, que es el conjunto de carteras óptimas que ofrecen el mayor rendimiento esperado posible para un nivel de riesgo definido.

2.1. El Rigor Matemático y las Fórmulas Clave

El rendimiento esperado de la cartera ($E(R_p)$) es una suma simple, pero el riesgo (varianza $\sigma_p^2$) es mucho más complejo debido a la covarianza:

$$E(R_p) = \sum_{i} w_i \cdot E(R_i)$$

$$\sigma_p^2 = \sum_{i} w_i^2 \sigma_i^2 + \sum_{i} \sum_{j \neq i} w_i w_j \sigma_i \sigma_j \rho_{ij}$$

Donde $w_i$ es el peso del activo $i$ en la cartera, $\sigma_i$ es su desviación estándar y $\rho_{ij}$ es el coeficiente de correlación entre los activos $i$ y $j$.

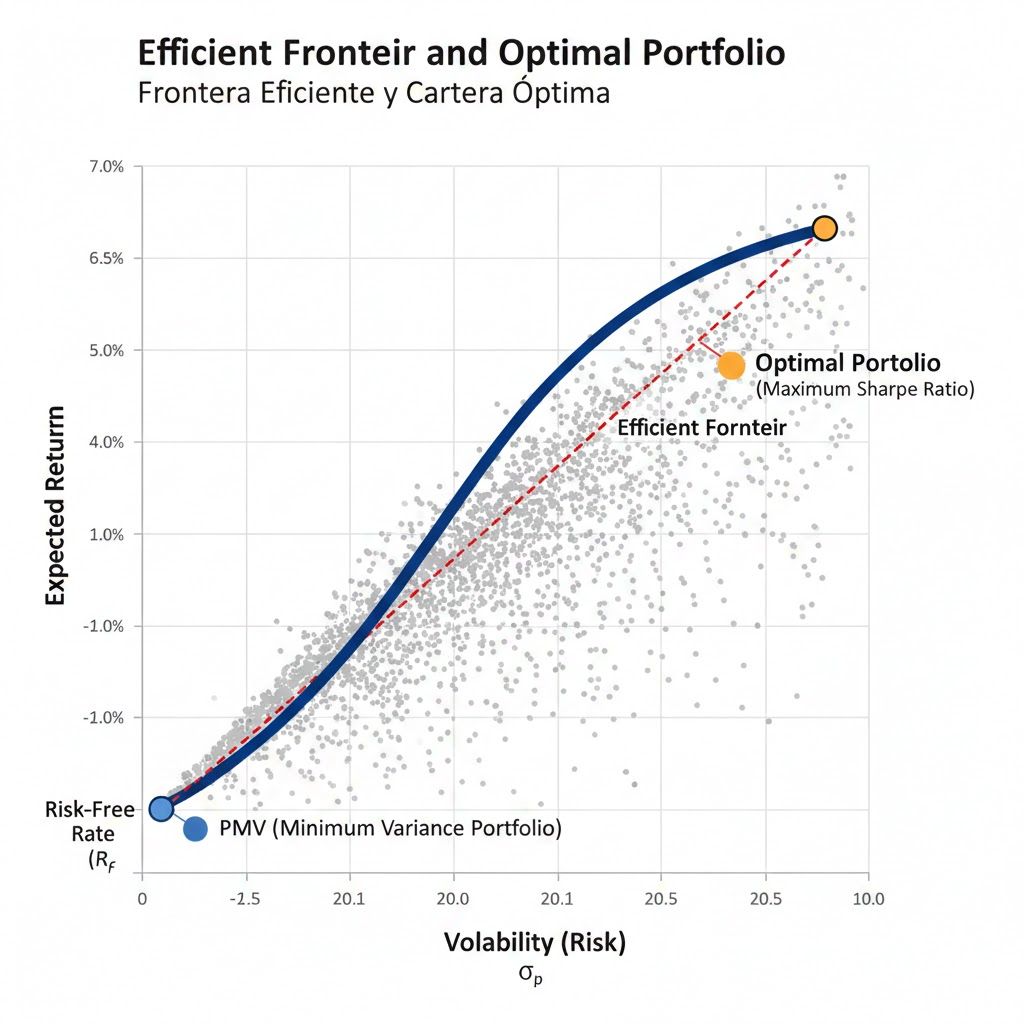
2.2. Simulación y Búsqueda de la Cartera Ideal

Para construir esta curva en la práctica, los analistas utilizamos la Simulación de Monte Carlo. Generamos aleatoriamente cientos o miles de combinaciones de ponderaciones de activos y graficamos el resultado de cada una en un plano de riesgo-rendimiento. La curva superior de este gráfico es la Frontera Eficiente.

Esta simulación nos permite identificar tres puntos cruciales que definen la estrategia de inversión:

Portafolio de Mínima Varianza (PMV): El punto en la frontera con el menor riesgo total posible. Es la opción preferida por fondos de pensiones o inversores que priorizan la preservación de capital sobre el crecimiento.
Portafolio Tangencial (Portafolio Óptimo): Este es el punto de tangencia de la Línea del Mercado de Capitales (CML) con la Frontera Eficiente. Es la cartera con la mejor relación riesgo-recompensa, medida por el Ratio de Sharpe.
El Ratio de Sharpe: Esta métrica es la joya de la corona de la MPT. Es la vara que mide la eficiencia de la gestión: cuánto rendimiento adicional se logra por cada unidad de riesgo asumida. Un gestor de cartera siempre aspira a maximizar este ratio.

4. La Perspectiva de cripTor: Limitaciones de la MPT en la Inversión Moderna

Si bien la MPT es fundamental, nuestro equipo de análisis insiste en que su aplicación ciega en los mercados de 2025 puede ser peligrosa, especialmente en el ámbito de las criptomonedas y las acciones de alta tecnología.

La MPT fue creada en un mundo donde el mercado se movía más lento y las distribuciones de precios eran más «normales». El mundo de hoy exige adaptaciones.

Limitación Clave: La Asunción de la Distribución Normal (Las Colas Gruesas): La MPT asume implícitamente que los rendimientos se distribuyen normalmente. Nuestra experiencia en el mercado de criptoactivos nos demuestra que esto es falso. Los rendimientos tienen «colas gruesas,» lo que significa que los eventos extremos (cisnes negros) son mucho más frecuentes de lo que predice la curva normal. Esto hace que el riesgo calculado por la MPT sea a menudo subestimado.
Limitación Clave: La Dependencia de Datos Históricos: Se utiliza la covarianza pasada para predecir la covarianza futura. En un mercado dominado por la IA y la macroeconomía global cambiante, esta presunción es obsoleta. Una recesión o una nueva regulación cripto pueden cambiar las correlaciones de la noche a la mañana.
La Cuestión Cripto Específica: En un portafolio que incluye Bitcoin, DeFi tokens o NFTs, el riesgo de liquidez y los costos de transacción pueden ser altos, variables que la MPT clásica ignora por completo.

5. La Evolución: MPT Aumentada con IA y Análisis Cuantitativo

La MPT no debe ser descartada, sino aumentada. Nuestro enfoque en cripTor es combinar la robustez de la MPT con el poder de predicción de la tecnología moderna:

Modelos de Volatilidad Dinámica (GARCH): En lugar de usar una desviación estándar simple y estática, empleamos modelos como GARCH (Generalized Autoregressive Conditional Heteroskedasticity) que permiten que la volatilidad y, por lo tanto, el riesgo, cambie con el tiempo, reflejando mejor los ciclos de mercado.
Optimización Robusta y Cuadrática: Utilizamos herramientas de optimización que añaden restricciones de negocio (costos de transacción, límites de liquidez) directamente a las ecuaciones de Markowitz, resultando en carteras que son más prácticas de implementar.
El Papel de la Inteligencia Artificial: La IA no reemplaza la MPT, sino que la alimenta. Los algoritmos de Machine Learning pueden analizar miles de variables macroeconómicas y de sentimiento para predecir correlaciones futuras con mayor precisión que los simples datos históricos, haciendo que el insumo principal de la MPT sea más inteligente.

Esta combinación de la sabiduría de Markowitz con la tecnología moderna es lo que define la gestión de carteras en el siglo XXI: precisión, adaptabilidad y una visión de riesgo más honesta.

Conclusión: La MPT como Punto de Partida, no de Llegada

La Teoría Moderna del Portafolio sigue siendo un concepto central en la gestión de inversiones. Su mayor legado es la enseñanza de que el riesgo de un activo no se evalúa de forma aislada, sino en el contexto de su relación con el resto de la cartera.

Para los gestores cuantitativos y los inversores sofisticados de hoy, la MPT es la base conceptual. Sin embargo, es imprescindible complementarla con modelos dinámicos, técnicas de optimización robusta y las predicciones alimentadas por Inteligencia Artificial para asegurar que la cartera es eficiente, no solo en teoría, sino en la realidad volátil del mercado.

Nuestro consejo final: Nunca confíes ciegamente en una única teoría. Utiliza la MPT para estructurar tu pensamiento, pero siempre valida sus supuestos con las herramientas de la tecnología moderna.